Temas Dados y Devatido En Clase

Publicado por: Yerico Jaén

Lógica Proposicional

Esta es una rama de la lógica clásica, se encarga de estudiar las preposiciones y trata sobre:
 verdad o la falsedad de las proposiciones y de cómo la verdad se transmite de unas proposiciones (premisas) a otras (conclusión). Una proposición es la unidad mínima de significado susceptible de ser verdadera o falsa.

Ejemplos dados en clases:

- Los perros Tienen 4 Patas                A es B
- Una gallina no es un Perro                C no es A
- Una gallina no tiene 4 patas             C no es B

- Una auto tiene 4 ruedas                    A es B
- Una moto no es un auto                    C no es B
- Una moto no tiene 4 ruedas             C no es A

Que es una Preposición?

Es la rama de la lógica clasica que estudia las proposición o sentencias lógicas posible si es verdad

 Las preposiciones generalmente tienen la función de introducir adjuntos, y en ocasiones también complementos obligatorios ligando el nombre o sintagma nominal al que preceden inmediatamente con un verbo u otro nombre que las antecede. En algunas lenguas las preposiciones pueden no encabezar un sintagma preposicional, como en inglés, donde incluso pueden aparecer al final de la frase.

Ejemplo, la palabra equivalente que aparece detrás y no delante se llama postposición.

Tradicionalmente, la gramática del español la ha definido como la parte invariable de la oración que une palabras denotando la relación que tienen entre sí.

Proposiciones Atómicas:

Las proposiciones atómicas (simples o elementales) carecen de conjunciones gramaticales típicas o conectivas (‘y’, ‘o’, ‘si... entonces’, ‘si y sólo si’) o del adverbio denegación ‘no’. Es una proposición que expresa que una cosa tiene una determinada propiedad o que unas cosas tienen una determinada relación.

Ejemplo

Hoy es jueves y tenemos clase

San Marcos es la universidad más antigua de América.

Un computador es una herramienta muy útil.

Las proposiciones Atómicas pueden ser clasificadas en:

• Las proposiciones predicativas constan de sujeto y predicado.

 Ejemplos:

a) El número 2 es par.

b) El espacio es relativo.

• Las proposiciones relacionales constan de dos o más sujetos

Vinculados entre sí.

 Ejemplos:

a) Silvia es hermana de Angélica.

b) 5 es mayor que 3.

c) José es amigo de la seguridad de la Universidad  

Colectores Preposicionales:

Son términos sin categorematicos  que se usan para modificar. Las preposiciones más utilizadas son las negaciones (¬) la representa la partícula lingüística (no) o cualquier otra partícula que incluya la negación.

Ejemplo:

¬ La casa no es Grande

¬ Mi tía no sabe manejar

¬ La Fula colonense no dice nada

Moleculares:

Están formadas por preposiciones atómicas o diferentes términos  sicategorematia

Ejemplo:

Ho es jueves y tenemos clase

Mañana es sábado y hay examen

Esta mañana no y en la noche si 

 Disyunciones Exclusivas:

“--” Expresa la idea que la verdad de un miembro es compatible con la verdad de la otra pero no las 2

Ejemplo:

El día esta lluvioso o nublado

La noche esta fría o calurosa  

Los Conectores proposicionales

Los conectores proposicionales son términos sicatogeromaticos que se usan para modificar o enlazar preposiciones.

Conectiva	Expresión en el lenguaje natural	Ejemplo	Símbolo en este artículo	Símbolos alternativos
Negación	no	No está lloviendo.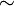
Conjunción	y	Está lloviendo y está nublado.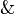
Disyunción	o	Está lloviendo o está soleado.
Condicional material	si... entonces	Si está soleado, entonces es de día.
Bicondicional	si y sólo si	Está nublado si y sólo si hay nubes visibles.
Negación conjunta	ni... ni	Ni está soleado ni está nublado.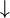
Disyunción excluyente	o bien... o bien	O bien está soleado, o bien está nublado.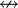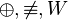

 Cuadro tomado de: http://es.wikipedia.org/wiki/L%C3%B3gica_proposicional


Tabla de verdad

Negación

Conjunción

Disyunción

Condicional

Bicondicional

Tabla de Equivalencia 

Ley	Equivalencia	Intro.
Identidad	P _ F = P P ^ T = P
Dominación	P _ T = T P ^ F = F
Conmutativa	(P ^ Q) ⇆ (Q ^ P) (P v Q) ⇆ (Q v P)	Esta ley puede aplicarse con tres de los cuatros conectivos diádicos: conjunción, disyunción y incondicional.
Indepotente	P _ P = P P ^ P = P
Doble Negación	P ⇆ (~~P)	Una proposición doblemente negada es igual a su afirmación y viceversa.
Asociativa	[(P v Q) v R] ⇆ [P v (Q v R)] o bien [(P ^ Q) ^ R] ⇆ [P ^ (Q ^ R)]	Esta ley ordena de diversas formas sin alterar los productos, cuando se tenga el mismo conectivo lógico, ya sea la conjunción o disyunción.
Distributiva	[(P v Q) ^ R] ⇆ [(P ^ R) v (Q ^ R) [(P ^ Q) v R)] ⇆ [(P v R) ^ (Q v R)	Se aplican cuando se tienen dos conectivos diferentes: conjunción - disyunción o bien disyunción -conjunción. Distribuye a la proposición fuera del paréntesis con las que están dentro de este.
Morgan	[~( P ^ Q)] ⇆ (~P v ~Q) [~(P v Q)] ⇆ (~P ^ ~Q)	Tiene dos formas en las que se puede aplicar la ley. A partir de una proposición en conjunción negada, se puede obtener la negación de cada uno de los conjuntivos pero cambiando el conectivo a disyunción, pero cambiando el conectivo a conjunción.
Absorción	P → Q /.˙. P → (P v Q)	Permite que a partir de una proposición condicional, se concluya en otra condicional con el mismo antecedente, aunque en el consecuente se unen las dos proposiciones con una conjunción.
Negación	p∨﹁p≡T p∧﹁p≡F

 Cuadro por: Yerico Jaen

fuente  del articulo http://es.wikipedia.org/wiki/Tabla_de_verdad



Archivo Word para descargar --- http://1drv.ms/1CHaM3A